UNIDAD DIDÁCTICA 10. OPERACIONES FINANCIERAS. EL INTERÉS . Y DESCUENTO
UNIDAD DIDÁCTICA 10. OPERACIONES FINANCIERAS. EL INTERÉS
INDICE
0. INTRODUCCIÓN
1. SISTEMAS DE CAPITALIZACIÓN
2. CAPITALIZACIÓN SIMPLE
3. EQUIVALENCIA FINANCIERA SIMPLE
4. DESCUENTO
5. CAPITALIZACIÓN COMPUESTA
6. EQUIVALENCIA FINANCIERA COMPUESTA
1º DÍA
En esta unidad aprenderemos como a través de las matemáticas financieras podemos trasladar en el tiempo los capitales que intervienen en
operaciones comerciales y financieras.
Cuando
se dispone de una cantidad de dinero se puede destinar a gastarlo o a
invertirlo para recuperarlo en un futuro más o menos próximo. De la misma
manera que estamos dispuestos a gastarlo para satisfacer una necesidad,
estaremos dispuestos a invertir siempre y cuando la compensación económica nos
resulte suficiente.
En
este sentido el principio básico de la
preferencia de liquidez establece que, a igualdad de cantidad, los bienes
más cercanos en el tiempo son preferidos a los disponibles en momentos más
lejanos. Este principio se suele expresar en matemáticas financiera como “un
euro hoy es mejor que un euro mañana”.
Por
ejemplo, si pido un préstamo a día de hoy por 100€ y tengo que devolverlo
dentro de 1 año. ¿Devolveré 100 € o más? MASSS, porque el valor futuro del dinero
es superior al del presente.
De la
misma manera, si nos dicen que cobraremos 100€ pero dentro de 1 año y los
quisiéramos adelantar a día de hoy, ¿me darían 100? No, nos darían menos de
100€ por adelantarlo a día de hoy.
Esto
es lo que vamos a aprender en esta unidad, que el valor actual del dinero es
diferente al valor futuro o lo que llamaremos valor final
Al
movimiento de capitales del presente al futuro lo llamaremos capitalización.
Y
cuando traemos capitales del futuro al presente lo llamaremos descuento.
Antes de empezar a profundizar, vemos este vídeo introductorio.
Aprovechamos para preguntar las dudas
¿QUE ES UN CAPITAL FINANCIERO?
Aprovechamos para preguntar las dudas
¿QUE ES UN CAPITAL FINANCIERO?
2º DÍA
1. Sistemas de capitalización
El interés se puede definir como la
retribución por el aplazamiento en el tiempo del consumo, esto es, el precio
por el alquiler o uso del dinero durante un período de tiempo.
Esta
compensación económica del interés, se exige por tres razones básicas:
- Por
el riesgo que se asume.
- Por la falta
de disponibilidad que supone desprenderse del capital durante un tiempo.
- Por
la depreciación del valor del dinero
en el tiempo.
La
cuantificación de esa compensación económica, de los intereses, depende de: a
cuantía del capital invertido, el tiempo que dura la operación y el tanto de
interés al que se acuerda la operación.
Capitalizar es llevar un capital a un momento futuro, teniendo en cuenta el tipo de interés del dinero, mientras que actualizar es traer un capital que está en el futuro al momento actual.
Se pueden diferenciar dos tipos de capitalización: la simple y la compuesta. En la simple partimos de la base de que no se reinvierten los intereses que se van generando, en la compuesta normalmente es a más de un año y sí que se reinvierten los intereses.
Las
operaciones en régimen de capitalización
simple se caracterizan porque los intereses a medida que se van generando
no se acumulan y no generan intereses en períodos siguientes (no son
productivos). De esta forma los intereses que se producen en cada período se
calculan siempre sobre el mismo capital (el inicial), al tipo de interés
vigente en cada período. Este régimen financiero es propio de operaciones a
corto plazo (menos de un año).
Partiendo
de un capital (C0) del que se dispone inicialmente (capital inicial),
se trata de determinar la cuantía final (Cn) que se recuperará en el
futuro sabiendo las condiciones en las que la operación se contrata (tiempo “n”
y tipo de interés “i”).
Este
capital final o montante se irá formando por la acumulación al capital inicial
de los intereses que genera la operación periódicamente y que, al no disponerse
de ellos hasta el final de la operación, se añaden finalmente al capital
inicial.
Los
intereses no son productivos, lo que significa que:
- A
medida que se generan no se acumulan al capital inicial para producir nuevos
intereses en el futuro y, por tanto
- Los
intereses de cualquier período siempre los genera el capital inicial, al tanto
de interés vigente en dicho período.
Para
actualizar de forma simple, despejaríamos en la ecuación el capital en el valor
actual, obteniendo la siguiente expresión:
Co
= Cn / (1 + n x i)
Escuchamos y vemos este vídeo y repasamos la teoría para familiarizarnos con las formulas y conceptos nuevos.
CAPITALIZACIÓN SIMPLE
CAPITALIZACIÓN SIMPLE
1º TAREA
ejercicios del libro del 1 al 11 incluido
En el libro en la parte de la teoría tb tenéis unos 13 ejercicios resueltos para que afiancéis los conceptos.
MIÉRCOLES 25 MARZO
3º DIA
REPASO Y DUDAS CON LOS EJERCICIOS( aquí os pongo un ejemplo de cada uno resuelto)
1º intentad hacedlo y luego comprobáis la solución.
2. Capitalización simple
Ya hemos visto que una Operación financiera es la sustitución de un capital presente por otro equivalente con vencimiento posterior, mediante la aplicación de la ley financiera en régimen de simple.
1.¿Cómo?
Partiendo de un capital (C0) del que se dispone inicialmente -capital inicial-, se trata de determinar la cuantía final (Cn) que se recuperará en el futuro sabiendo las condiciones en las que la operación se contrata (tiempo -n- y tipo de interés -i-).
Este capital final o montante se irá formando por la acumulación al capital inicial de los intereses que genera la operación periódicamente y que, al no disponerse de ellos hasta el final de la operación, se añaden finalmente al capital inicial.
2.Características de la operación
Los intereses no son productivos, lo que significa que:
- A medida que se generan no se acumulan al capital inicial para producir nuevos intereses en el futuro y, por tanto
- Los intereses de cualquier período siempre los genera el capital inicial, a ltanto de interés vigente en dicho período.
Gráficamente para una operación de tres períodos:
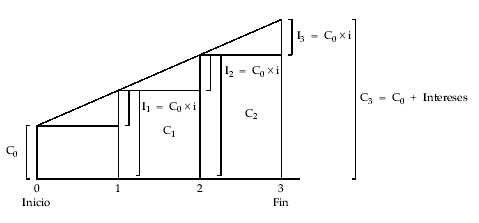
3. Desarrollo de la operación
El capital al final de cada período es el resultado de añadir al capital existente al inicio del mismo los intereses generados durante dicho período. De esta forma, la evolución del montante conseguido en cada momento es el siguiente:
| Momento 0: C0
Momento 1: C1 = C0 + I1 = C0 + C0x i = C0x (1 + i)
Momento 2:
C2 = C0 + I1 + I2 = C0 + C0x i + C0x i = C0x (1 + 2 i)
Momento 3:
C3 = C0 + I1 + I2 + I3 = C0 + C0x i + C0x i + C0 i = C0x (1 + 3 i)
…
Momento n:
Cn = C0 + I1 + I2 + … + In = C0 + C0x i + … + C0x i = C0 + C0x nx i |
| Cn = C0 x (1 + n x i) |
Expresión aplicable cuando el tipo de interés de la operación se mantiene constante todos los períodos.
A partir de la expresión anterior (denominada fórmula fundamental de la capitalización simple) no solamente se pueden calcular montantes sino que, conocidos tres datos cualesquiera, se podría despejar el cuarto restante.
Finalmente, hay que tener en cuenta que «n» lo que indica es el número de veces que se han generado (y acumulado) intereses al capital inicial, por tanto, esa variable siempre ha de estar en la misma unidad de tiempo que el tipo de interés (no importando cuál sea).
EJEMPLO 1
Calcular el montante obtenido al invertir 2.000 euros al 8% anual durante 4 años en régimen de capitalización simple.
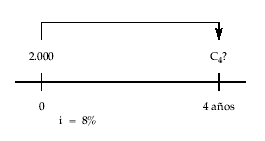
C4 = 2.000 x (1 + 4 x 0,08 ) = 2.640 €
EJEMPLO 2
Se quiere conocer qué capital podremos retirar dentro de 3 años si hoy colocamos 1.000 euros al 5% de interés anual para el primer año y cada año nos suben el tipo de interés un punto porcentual.
En este caso la fórmula general de la capitalización simple no es aplicable al ser diferente el tipo de interés en cada período. El montante será, igualmente, el resultado de añadir al capital inicial los intereses de cada período, calculados siempre sobre el capital inicial pero al tipo vigente en el período de que se trate.
C3 = C0 + I1 + I2 + I3 = 1.000 + 1.000 x 0,05 + 1.000 x 0,06 + 1.000 x 0,07 = 1.180 €
4. Cálculo del capital inicial
Partiendo de la fórmula de cálculo del capital final o montante y conocidos éste, la duración de la operación y el tanto de interés, bastará con despejar de la misma:
Cn = C0 x (1 + n x i)
despejando C0 resulta:
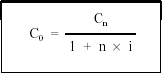
EJEMPLO 3
¿Cuánto deberé invertir hoy si quiero disponer dentro de 2 años de 1.500 euros para comprarme un coche, si me aseguran un 6% de interés anual para ese plazo?
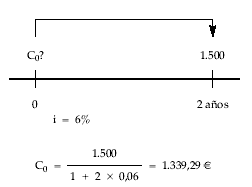
5 . Cálculo de los intereses totales
Bastará con calcular los intereses de cada período, que siempre los genera el capital inicial y sumarlos.
Intereses totales = I1 + I2 + … + In = C0x i1 + C0x i2 + … + C0x in
| C0 x (i1 + i2 + … + in) |
Si i1 = i2 = … = in = i se cumple:
Intereses totales = I1 + I2 + … + In = C0x i + C0x i + … + C0x i
| C0 x i x n |
Conocidos los capitales inicial y final, se obtendrá por diferencias entre ambos:
| In = Cn – C0 |
EJEMPLO 4
¿Qué intereses producirán 300 euros invertidos 4 años al 7% simple anual?
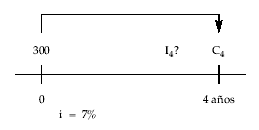
Por suma de los intereses de cada período:
Intereses totales = I1 + I2 + I3 + I4 = C0x i + C0x i + C0x i + C0x i = C0 x i x 4 = 300 x 0,07 x 4 = 84 €
También se puede obtener por diferencias entre el capital final y el inicial:
C4 = 300 x (1 + 0,07 x 4) = 384In = 384 – 300 = 84 €
EJEMPLO 5
¿Qué interés producirán 6.000 euros invertidos 8 meses al 1% simple mensual?
In = C0 x i x n = 6.000 x 0,01 x 8 = 480 €
6 . Cálculo del tipo de interés
Si se conocen el resto de elementos de la operación: capital inicial, capital final y duración, basta con tener en cuenta la fórmula general de la capitalización simple y despejar la variable desconocida.
Cn = C0 x (1 + n x i)
Los pasos a seguir son los siguientes:
Pasar el C0 al primer miembro:
Pasar el 1 al primer miembro (restar 1 en los dos miembros):
Despejar el tipo de interés, dividiendo por n la expresión anterior:
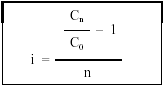
EJEMPLO 6
Determinar el tanto de interés anual a que deben invertirse 1.000 euros para que en 5 años se obtenga un montante de 1.500 euros.
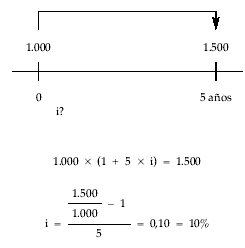
7. Cálculo de la duración
Conocidos los demás componentes de la operación: capital inicial, capital final y tipo de interés, partiendo de la fórmula general de la capitalización simple y despejando la variable desconocida.
Punto de partida:
Cn = C0 x (1 + n x i)
Pasar el C0 al primer miembro (dividir por C0 la ecuación anterior):
Cn— = 1 + n x iC0
Pasar el 1 al primer miembro (restar 1 a los dos miembros):
Cn— – 1 = n x iC0
Despejar la duración n, dividiendo por i:
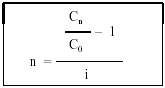
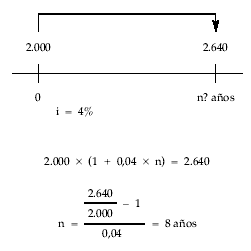
EJEMPLO 7
Un capital de 2.000 euros colocado a interés simple al 4% anual asciende a 2.640 euros. Determinar el tiempo que estuvo impuesto.
8. ¿QUÉ DOS PROBLEMAS NOS VAMOS A ENCONTRAR?
1º LAS UNIDADES PARA LAS OPERACIONES DEBEN SER HOMOGENEAS
HABRÁ MOMENTOS EN LAS QUE EL TIEMPO "n" VENGA EN AÑOS, Y EL TIPO DE INTERÉS O RÉDITO EN MESES "t"
Vemos este vídeo y luego hacemos los ejercicios:
enlace del video:
INTERESES Y TIEMPO EN LAS MISMAS UNIDADES
ACTIVIDAD
8. En la siguiente tabla calcula el dato que falta de cada fila utilizando el interés simple.
JUEVES 26 MARZO 4º DIA
LO IMPORTANTE DEL EJERCICIO 8 ES APRENDER A PONER EL TIEMPO Y EL TIPO DE INTERÉS EN LAS MISMAS UNIDADES.
- Para ello vamos a ver de nuevo el vídeo: ENLACE
INTERÉS Y TIEMPO EN UNIDADES HOMOGÉNEAS
- Luego vamos a ver el apartado 1 y 2 que os he hecho en el cuaderno y subido en una foto.
- A continuación compruebo que he puesto en cada apartado del ejercicio de ayer, las mismas unidades de tiempo y de interés. Como el 90% no lo habéis hecho, los hago otra vez.
Esa es la tarea de hoy
Recordad tiempo y tipo de interés o rédito en unidades homogéneas.
ejercicio 8 en unidades homogéneas
8. En la siguiente tabla calcula el dato que falta de cada fila utilizando el interés simple.
5ºDIA VIERNES 27 MARZO
Ya sabemos poner el interés y el tiempo en las mismas unidades.
2º PROBLEMA. CALCULO DE INTERESES EQUIVALENTES: calculo de intereses en periodos inferiores al año: trimestral, cuatrimestral, semestral...
¿Para que utilizamos esto? Por ejemplo cuando vamos al banco y nos ofrecen un interés anual, pero pagadero trimestralmente. Es para esto que tenemos que saber calcular cuanto nos van a dar trimestralmente y por supuesto siempre equivalente al interés anual.
Que vamos a calcular: intereses fraccionados trimestral, cuatrimestral, semestral... equivalentes al año.
Los tantos de interés equivalentes en simple son proporcionales, es decir, cumplen la siguiente expresión:
i = ik *k
donde k se denomina frecuencia de capitalización y se define como el número de partes iguales en las que se divide el periodo de referencia (considerando como tal el año), pudiendo tomar los siguientes valores:
k = 2 (semestre) i2 = tanto de interés semestral
k = 3 (cuatrimestre) i3 = tanto de interés cuatrimestral
k = 4 (trimestre) i4 = tanto de interés trimestral
k = 12 (mes) i12 = tanto de interés mensual
Determinar el montante resultante de invertir 700 euros durante tres años en las siguientes condiciones:
Cn = C0*(1 + i * n)
a) Interés simple anual del 12 por 100:
Cn = 700 *(1 + 3 *0,12) = 952
b) Interés simple semestral del 6 por 100:
Cn = 700 * (1 + 3 0,06 *2) = 952
c) Interés simple mensual del 1 por 100:
Cn = 700 * (1 + 3 0,01 * 12) = 952
Este apartado lo he cogido de libro Paraninfo, por si allí lo veis mas claro.
Capitalización no anual
A veces el tipo de interés
no viene expresado en años sino en meses, días, trimestres, etc. (tipo de
interés mensual, diario, trimestral, etc.).Para realizar los cálculos
correctamente aplicando las fórmulas que hemos visto, el tipo de interés y el
tiempo deben expresarse en la misma unidad de tiempo:
si el tanto es anual, el
tiempo debe expresarse en años;
si el tanto es mensual, el
tiempo debe expresarse en meses, etc.
A los tantos unitarios
equivalentes a una fracción de año se les llama tantos fraccionados:
si llamamos i al tanto anual,
i12 sería el tanto mensual,
i365 sería el tanto diario;
Tantos equivalentes
Dos tantos son equivalentes
cuando aplicados al mismo capital inicial durante el mismo tiempo, el capital
final es el mismo
No os preocupéis en el vídeo hay una repaso de la teoría y un ejercicio explicado;
ENLACE DEL VÍDEO:
Cálculo de INTERESES EQUIVALENTES
ACTIVIDADES DEL LIBRO
U.D 10. EJERCICIOS DEL 12-15 ( si ya has hecho los 11 primeros)
LUNES - MARTES 30 MARZO 6º DIA
( COMO ES DENSO E IMPORTANTE TENÉIS DOS DÍAS, LUNES Y MARTES PARA ESTA PARTE)
Antes de empezar con los ejercicios os recomiendo que veáis el vídeo sobre el descuento: ENLACE
https://www.youtube.com/watch?v=fIVpspvy6y0&t=26s
Esta parte se corresponde con El descuento y Valor Efectivo del libro, si lo necesitáis me lo pedís y lo subo tb.
Podéis hacer los ejemplos del tema que vienen resueltos y aclaran los conceptos, son el 10.17, 10.18, 10.19, 10.20, 10.21, 10.22.
TAREA: ACTIVIDADES: 23 al 26 del libro de Paraninfo, los subo al apartado de ejercicios, para los que no lo tengáis.
https://youtu.be/uJSYO_hz4l8
AQUÍ INCLUYO UN NUEVO VÍDEO PARA ACLARAR LAS DUDAS
31 MARZO , MARTES- MIÉRCOLES 7º dia
U.D 10. EJERCICIOS DEL 12-15 ( si ya has hecho los 11 primeros)
LUNES - MARTES 30 MARZO 6º DIA
( COMO ES DENSO E IMPORTANTE TENÉIS DOS DÍAS, LUNES Y MARTES PARA ESTA PARTE)
3. OPERACIONES DE
DESCUENTO
Las operaciones de descuento son aquellas que realizan
las empresas, mediante las que una
entidad financiera le anticipa el dinero que le deben
sus clientes.
El desarrollo de este proceso sería el siguiente:
1. Una empresa vende a un cliente, quedando una
cantidad pendiente de pago. Por este motivo,
se rellena una letra en la que figura este importe
(Nominal) y un plazo establecido para el pago
(Vencimiento de la operación).
2. La empresa vendedora desea disponer del dinero de
la venta anterior anticipadamente, para
ello acude a su banco para que le adelante el dinero
(operación de descuento).
La entidad bancaria le cobrará un tanto de interés
(tanto de descuento) que se calculará por los días que el banco le anticipa el dinero
(Días). El importe de la letra menos el importe de los intereses (Descuento)
será la cantidad que en este momento recibe la empresa (Efectivo). Como podemos
apreciar, es una operación similar a un préstamo con la garantía de la letra.
3. Llegado el vencimiento
de la letra, si el banco cobra la letra del cliente, se producirá la
finalización de la
operación quedando en poder de la entidad bancaria este importe. Si la letra no
es
pagada, la empresa
vendedora deberá devolver al banco el importe de la letra.
A este procedimiento se le
llama descuento de letra o negociación de una letra. Para realizar esta
operación previamente se ha
tenido que acordar con el banco las condiciones que se van a aplicar y cuál es
el importe máximo de letras descontadas que la empresa puede tener. A este
acuerdo, entre la entidad bancaria y la empresa, se denomina línea de
descuento.
Elementos que intervienen
- NOMINAL (N): Cantidad que
queda pendiente en la operación. Es el importe de la letra. ( VALOR FINAL)
- TIEMPO (n): Días que
transcurren desde que se realiza la operación hasta el vencimiento de la
operación.
- TANTO DE DESCUENTO (i) =
Es el tanto de interés anual que se aplica a la operación.
- DESCUENTO (D) = Intereses
totales de la operación. Para calcularlos existen dos formas:
descuento comercial o
bancario y el descuento racional o matemático.
- EFECTIVO (E): Es el
importe que se recibe anticipadamente. (VALOR INICIAL).
Para calcularlo, al Nominal le restamos el descuento. EFECTIVO = NOMINAL – DESCUENTO
Para calcularlo, al Nominal le restamos el descuento. EFECTIVO = NOMINAL – DESCUENTO
https://www.youtube.com/watch?v=fIVpspvy6y0&t=26s
Esta parte se corresponde con El descuento y Valor Efectivo del libro, si lo necesitáis me lo pedís y lo subo tb.
Podéis hacer los ejemplos del tema que vienen resueltos y aclaran los conceptos, son el 10.17, 10.18, 10.19, 10.20, 10.21, 10.22.
TAREA: ACTIVIDADES: 23 al 26 del libro de Paraninfo, los subo al apartado de ejercicios, para los que no lo tengáis.
https://youtu.be/uJSYO_hz4l8
AQUÍ INCLUYO UN NUEVO VÍDEO PARA ACLARAR LAS DUDAS
31 MARZO , MARTES- MIÉRCOLES 7º dia
(ESTA PARTE LA AÑADÍS A LA CARPETA ENTRE EL MARTES O MIÉRCOLES, SEGÚN VAYÁIS)
4. Equivalencia
financiera
Se
entiende por operación financiera la
sustitución de uno o más capitales por otro u otros equivalentes en distintos
momentos de tiempo, mediante la aplicación de una ley financiera.
En
definitiva, cualquier operación financiera se reduce a un conjunto de flujos de
caja (cobros y pagos) de signo opuesto y distintas cuantías que se suceden en
el tiempo. Así, por ejemplo, la concesión de un préstamo por parte de una
entidad bancaria a un cliente supone para este último un cobro inicial (el
importe del préstamo) y unos pagos periódicos (las cuotas) durante el tiempo
que dure la operación. Por parte del banco, la operación implica un pago
inicial único y unos cobros periódicos.
La
realización de una operación financiera implica, por tanto, que se cumplan tres
puntos:
- Sustitución de capitales. Ha de existir
un intercambio de unos capitales por otros.
- Equivalencia. Los capitales han de ser
equivalentes, es decir, debe resultar de la aplicación de una ley financiera.
- Aplicación de una ley financiera. Debe
existir acuerdo sobre la forma de determinar el importe de todos y cada uno de
los capitales que compongan la operación, resultado de la consideración de los
intereses generados.
Es
importante destacar que el concepto de equivalencia no significa que no haya
ganancia o coste en la operación. Todo lo contrario, la equivalencia permite
cuantificar ese beneficio o pérdida que estamos dispuestos a asumir en una
operación concreta.
Para
que una operación financiera se realice es necesario que a los sujetos
intervinientes las cuantías que dan y reciben les resulten equivalentes. Es
necesario que deudor y acreedor se pongan de acuerdo en cuantificar los
capitales de los que se parte y a los que finalmente se llega. Esto implica
elegir un método matemático que permita dicha sustitución: una ley financiera.
La ley financiera se define como un modelo matemático (una fórmula) para
cuantificar los intereses por el aplazamiento y/o anticipación de un capital en
el tiempo.
Conociendo
las diferentes leyes financieras que existen y cómo funcionan se podrán
sustituir unos capitales por otros, pudiéndose formalizar las diferentes
operaciones financieras.
Así,
cuando se dispone de varios capitales de diferentes cuantías y situados en
diferentes momentos de tiempo puede resultar conveniente saber cuál de ellos es
más interesante desde el punto de vista financiero (porque valga más o menos
que los demás). Para decidir habría que compararlos, pero no basta con fijarse
solamente en las cuantías, se tendría que considerar, a la vez, el momento de
tiempo donde se encuentran situados. Además, la comparación debería ser
homogénea, es decir, tendrían que llevarse todos los capitales a un mismo
momento y ahí efectuar la comparación.
De
esta forma, comprobar la equivalencia
financiera entre capitales consiste en comparar dos o más capitales
situados en distintos momentos y, para un tipo dado, observando si tienen el
mismo valor en el momento en que se comparan. Para igualar los capitales en un
momento determinado se utilizará la capitalización o el descuento
(actualización).
Si
dos o más capitales se dice que son equivalentes resultará indiferente
cualquiera de ellos, no habiendo preferencia por ninguno en particular. Por el
contrario, si no se cumple la equivalencia habrá uno sobre el que tendremos
preferencia y, en consecuencia, lo elegiremos.
Si el
principio de equivalencia se cumple en un momento de tiempo concreto, no tiene
por qué cumplirse en otro momento cualquiera (siendo lo normal que no se cumpla
en ningún otro momento). Consecuencia de esta circunstancia será que la
elección de la fecha donde se haga el estudio comparativo afectará y
condicionará el resultado.
Para
ver si dos alternativas son financieramente equivalentes se tendrán que valorar
en un mismo momento de tiempo y obligar a que tengan las mismas cuantías. A
este momento de tiempo donde se realiza la valoración se le denomina época o
fecha focal o, simplemente, fecha de estudio.
Para
plantear una sustitución de capitales el acreedor y el deudor han de estar de
acuerdo en las siguientes condiciones fundamentales:
- Momento
de tiempo a partir del cual se computan los vencimientos.
- Momento
en el cual se realiza la equivalencia, teniendo en cuenta que al variar este
dato varía el resultado del problema.
- Tanto
de valoración de la operación.
- Decidir
si se utiliza la capitalización o el descuento.
Vamos a verlo mediante un ejemplo en el vídeo:
ENLACE VÍDEO CAPITALES EQUIVALENTES
U.D 10. EJERCICIOS 29 Y 30 del libro CORRESPONDEN A ESTA PARTE.
Vamos a verlo mediante un ejemplo en el vídeo:
ENLACE VÍDEO CAPITALES EQUIVALENTES
U.D 10. EJERCICIOS 29 Y 30 del libro CORRESPONDEN A ESTA PARTE.
JUEVES 2 ABRIL 8º dia
5. Capitalización compuesta
5. Capitalización compuesta
Por su parte, las operaciones en régimen capitalización compuesta se caracterizan porque los intereses, a diferencia de lo que ocurre en régimen de simple, a medida que se van generando pasan a formar parte del capital de partida, se van acumulando, y producen a su vez intereses en períodos siguientes (son productivos). En definitiva, lo que tiene lugar es una capitalización periódica de los intereses. De esta forma los intereses generados en cada período se calculan sobre capitales distintos (cada vez mayores ya que incorporan los intereses de períodos anteriores).
El capital final o montante (Cn) se va formando por la acumulación al capital inicial (C0) de los intereses que periódicamente se van generando y que, en este caso, se van acumulando al mismo durante el tiempo que dure la operación (n), pudiéndose disponer de ellos al final junto con el capital inicialmente invertido.
Los intereses son productivos, lo que significa que:
- A medida que se generan se acumulan al capital inicial para producir nuevos intereses en los períodos siguientes.
- Los intereses de cualquier período siempre los genera el capital existente al inicio de dicho período.
Gráficamente para una operación de tres períodos:

El capital al final de cada período es el resultado de añadir al capital existente al inicio del mismo los intereses generados durante dicho período. De esta forma, la evolución del montante conseguido en cada momento es el siguiente:
Cn = C0 x (1 + i)n
Al igual que en la capitalización simple, podríamos actualizar un capital Cn, despejando el valor actual de la fórmula anterior:
Este ejercicio del libro compara el mismo ejercicio en capitalización simple y compuesta.
40.
Luis y Antonio
invierten un capital de 3.000 € durante 3 años. Luis coloca su capital al 4 %
anual compuesto y Antonio al 4 % de
interés anual simple. Calcula el capital final obtenido por cada uno.
Ejemplos
1. Hallar el valor adquirido por 12.000 euros en 5 años al 6,5% de
interés anual.
Solución:
Sólo hay que aplicar
directamente la fórmula de la capitalización compuesta:
C = 12000(1 0,065) =
16.441,04 euros
2. Hace 4 años impusimos una cantidad en un banco que capitaliza al 5%
anual y hoy
tenemos 9.724,05 euro, ¿qué cantidad impusimos?
Solución:
Aplicaremos directamente la
fórmula de la capitalización compuesta, pero ahora
tendremos que despejar Co
3. Determine el tipo de
interés anual al que capitaliza un banco sabiendo que hace 7
años impusimos 20.000 euros
y hoy tenemos un montante de 22.973,71 euros.
*Solución:
Aplicaremos directamente la
fórmula de la capitalización compuesta y despejaremos
1+i, para luego calcular i:
Elevando los dos miembros a
1/7 conseguimos eliminar el exponente del primer
miembro
i = 0,02
En el apartado de ejercicios tenéis para resolver los del libro, del 31 al 34 son de capitalización compuesta.
*OS DEJO UN VÍDEO QUE EXPLICA COMO DESPEJAR EL INTERES PARA LOS EJERCICIOS: https://youtu.be/B7X6jotw2yc
9º dia VIERNES 3 ABRIL ( ANIMO ES NUESTRO ULTIMO DÍA, EL EMPUJÓN FINAL)
6. EQUIVALENCIA DE CAPITALES EN CAPITALIZACIÓN COMPUESTA
Para explicar la equivalencia de capitales voy a utilizar un ejemplo práctico de reunificación de deudas bajo el sistema de capitalización compuesta.
Si una empresa tiene tres deudas de 2.000, 4.000 y 5.000 euros con vencimientos a los 6, 8 y 10 años, respectivamente, podría llegar al acuerdo con el acreedor de sustituir las tres deudas por una sola a pagar a los 9 años.
Para calcular el importe a pagar en ese momento si la operación se concierta al 8% de interés compuesto anual, se realizaría una equivalencia de estos tres capitales en uno valorado en el noveno año, tal como se muestra en el siguiente esquema:
Por lo tanto, a un interés del 8%, es equivalente una deuda a nueve años por valor de 11.469,05, que tres deudas de 2.000, 4.000 y 5.000 euros a 6, 8 y 10 años respectivamente.
EJERCICIOS DE CAPITALIZACIÓN COMPUESTA 1
- Calcula el montante
producido por 40.000€ colocados al 8% anual durante cuatro años.
- Javier efectúa un
depósito bancario de 20.000 € a plazo fijo durante tres años, a un 9%
anual. Calcula la cantidad que recibirá al cabo de esos tres años.
- ¿Cuál fue el capital
que invertido a un 9% anual durante 5 años produjo un montante de 25.000
€.
- ¿Qué capital
tendremos que depositar en un banco al 8% anual para que en cuatro años
obtengamos un montante de 40.000€.
- Calcula los
intereses que le entregaremos a un prestamista dentro de dos años si hemos
recibido como préstamo en el día de hoy 50.000€ siendo el tipo de interés
el 9% anual.
- Una empresa ha
recibido hoy 100.000€ de préstamo a devolver dentro de cuatro años.¿Qué
cantidad entregará como intereses si el tipo de interés es el 10% anual?
- Calcula el tipo de
interés de un préstamo de 4.000.000 € durante dos años si el capital final
cargado en cuenta por el banco asciende a 5.000.000€
7.1. CAPITALIZACIÓN COMPUESTA CON INTERESES FRACCIONADOS
Para los que lo veáis por primera vez, esta parte puede parecer dura, os recomiendo escuchar los vídeos y hacer los ejercicios a la vez.
Al final os daréis cuenta que sabiendo aplicar la formula y distinguiendo los intereses, sale con facilidad.
Animo, se trata que reconozcáis y sepáis porque hay diferentes intereses en la publicidad de los bancos.
TANTO NOMINAL - TANTO EFECTIVO - TANTOS EQUIVALENTES
ENLACE: https://youtu.be/Wjxug8iybgM
ENLACE AL VÍDEO ACLARATORIO
https://youtu.be/h-eP8gsJB6I
Para los que lo veáis por primera vez, esta parte puede parecer dura, os recomiendo escuchar los vídeos y hacer los ejercicios a la vez.
Al final os daréis cuenta que sabiendo aplicar la formula y distinguiendo los intereses, sale con facilidad.
Animo, se trata que reconozcáis y sepáis porque hay diferentes intereses en la publicidad de los bancos.
TANTO NOMINAL - TANTO EFECTIVO - TANTOS EQUIVALENTES
ENLACE: https://youtu.be/Wjxug8iybgM
El
TIN (Tanto de Interés Nominal jm) es el porcentaje fijo
que se pacta como concepto de pago por el dinero prestado. Indica el tanto por
ciento que recibe el banco por ceder el dinero. Mientras que la TAE es el tipo de interés que indica el
coste o rendimiento efectivo de un producto.
Son conceptos establecidos por el Banco de España y, por tanto, oficiales.
El TIN es el tipo que los bancos utilizan y nos comunican
en los contratos de depósitos, imposiciones, préstamos, créditos e hipotecas, y
que refleja el pago de intereses por el cambio del valor del
dinero en un periodo de tiempo.
El Tipo de Interés Nominal (TIN) es el porcentaje fijo que se pacta como concepto de pago por el
dinero prestado. Indica el tanto por
ciento que recibe el banco por ceder el dinero.
El TIN no tiene en cuenta ningún tipo de gasto asociado a
la operación, únicamente es el interés que se ha acordado con la entidad
financiera para la operación. A diferencia de la TAE, el TIN no tiene por qué
ser anual.
TAE (Tasa Anual Equivalente), incluye, además del
interés, los gastos y comisiones bancarias de una operación financiera. Revela
el coste o rendimiento de un producto financiero y permite comparar distintos
productos.
VAMOS A VER UN VÍDEO ACLARATORIO Y REFLEJO DE LA REALIDAD:
Una vez visto el vídeo podemos comprender que en ausencia
de gastos y comisiones la TAE coincidirá con el tipo de interés efectivo (TIE).
- jm TIN, es un tanto nominal. (Es un tanto teórico).
- im TIE, es un tanto efectivo, y es el resultado de dividir el TIN ( jm) entre el número de capitalizaciones anuales (m).
im
= jm / m ó jm = im
* m
Para calcular la TAE de un préstamos podemos dirigirnos a la web
del Banco de España, donde disponemos de un simulador on line para poder hacer
los cálculos: https://app.bde.es/asb_www/tae.html#/principalTAE.
NOTA: Para operar tenemos que convertir el tanto nominal jm
en un tanto efectivo im, porque como hemos dicho jm es un
tanto teórico y no se puede operar con un tanto teórico sino con un tanto
efectivo.
TANTOS EQUIVALENTES
Dos tantos
expresados en distintas unidades de tiempo, son tantos equivalentes cuando
aplicados a un mismo capital inicial y durante un mismo período de tiempo
producen el mismo interés o generan el mismo capital final o montante.
Es decir un
capital de 1€ capitalizado 1 años a un interés i, dará un Cn:
Cn = C0
(1+i)n Cn
= 1 (1+i)1 (1+i)
Si ese mismo
capital de 1€ se impone a un interés fraccionado de im, durante 1
año, el capital final obtenido sería:
Cn = C0
(1+im)m Cn
= 1 (1+im)m (1+im)m
Por tanto para
que i sea equivalente a im, tendremos que igualar
ambos capitales finales:
(1+i)
= (1+im)m
Y a partir de esta igualdad podemos calcular el tanto efectivo
anual (TIE) i y el tanto efectivo
fraccionado im.
i = (1+im)m – 1
 |
|
ENLACE AL VÍDEO ACLARATORIO
https://youtu.be/h-eP8gsJB6I
Ejemplo
Veamos qué efectivo es
equivalente al 8% anual convertible por trimestres.
( toda esa frase se traduce en si j es 8% anual, calcula el trimestral: i`4, para ello divido el anual entre 4 por que son los trimestres que tiene un año)
j4=0,08, esto significa que se aplica el 2% trimestral.
Por la
fórmula general del interés compuesto, suponiendo C0=1 euro
tendremos al año (4 trimestres):
C4=
(1+0,02)4 = 1,0824
que es lo mismo que si hubiéramos
aplicado el 8,24% efectivo anual
Hay operaciones en que los cobros o los pagos no son anuales, por ejemplo
los créditos hipotecarios, en los que los pagos suelen ser mensuales. En esos
casos el banco aplica un interés periódico,
por ejemplo mensual en el caso de los créditos
hipotecarios, pero
¿ha visto Vd. algún anuncio de hipotecas en que se hable de interés
mensual? No, el tipo de interés siempre
se da anual, lo que hace el banco es multiplicar el tipo de interés que está
aplicando periódicamente por el número de períodos que tiene el año. Si en un
crédito hipotecario el banco aplica un 1% mensual dirá que está aplicando el
12% anual, pero eso no es del todo cierto, hay que matizarlo un poco.
Según hemos estudiado hasta ahora 1 euro invertido durante 12 meses al 1%
mensual se convertiría en
|
C = 1(1 + 0,01)12 = 1,1268 euros
Lo que significa que 1 euro de principio de año vale 1,1268 euros al
final de año, es decir que el interés del año es 0,1268, que es el 12,68% y no
el 12%. ¿Qué ha pasado?. Lo que ha pasado es que hay un interés anual efectivo,
que es el que habíamos estudiado hasta ahora y que siempre es anual, y hay un
tipo de interés nominal, que es el que hemos introducido ahora, que se dice
anual, pero que se aplica periódicamente y del que siempre hay que indicar el
período al que está referido. Esta indicación se hace diciendo ``capitalizable
por '' o ``convertible por ''
Como hemos visto el 12% nominal anual capitalizable por meses es el 1%
mensual aplicado durante 12 meses y, como también hemos visto el interés
efectivo que le corresponde es el 12,68% que es el que realmente pagamos.
También hablaremos, por ejemplo, del 12% nominal anual capitalizable por
semestres, lo cual significa que estamos aplicando el 6% semestral. ¿Qué tipo
de interés efectivo le corresponderá a éste?
|
C = 1(1+
0,06)2 = 1,1236
El tipo
efectivo correspondiente es el 12,36%.
Podríamos considerar otros muchos 12% nominales anuales convertibles por
trimestres, por cuatrimestres, por semanas o por días y encontraríamos que a
cada uno le corresponde un tipo efectivo distinto.
Por todo ello,
aunque los bancos den los tipos nominales lo que de verdad necesitamos saber
para comparar dos tipos de interés nominales son los efectivos
correspondientes. Recapitulemos:
Ejemplos
1.
Determine el tipo de interés mensual sabiendo que el
nominal anual capitalizable mensualmente es el
6%.
Solución:
En realidad conocer el tipo de interés nominal anual capitalizable por
meses es conocer el tipo de interés mensual, lo que pasa en que, en la
práctica, los tipos de interés siempre se dan en términos anuales, pero en este
ejemplo el banco está aplicando un interés mensual, que denotaremos por i12 :
i12 =j12/ 12
= 0,06
= 0,005
2. Determine
el tipo de interés semestral sabiendo que el nominal anual capitalizable
semestralmente es el 9%.
Solución:
i = j2 = 0,09 = 0,045
2 2 2
3. Determine
el tipo de interés nominal anual capitalizable por cuatrimestres equivalente al 3% efectivo anual
Solución
1
| ||
j3= (1+ 0,03)3 -1
| ||
El tipo efectivo
es siempre mayor que cualquier nominal equivalente. En este caso el efectivo es
el 3% y el nominal el 2,97%
4. Determine
el tipo de interés nominal anual capitalizable por trimestres equivalente al 4% efectivo anual
Solución: j`4

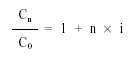
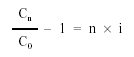











Comentarios
Publicar un comentario